Advent Calendar 2021
| Day 11 | Day 12 | Day 13 |
The gift is presented by Cheok-Yin Fung. Today he is talking about his solution to “The Weekly Challenge - 123”. This is re-produced for Advent Calendar 2021 from the original post by Cheok-Yin Fung.
Task #2: Square Points
You are given coordinates of four points i.e. (x1, y1), (x2, y2), (x3, y3) and (x4, y4).
Write a script to find out if the given four points form a square.
After seeing the task statements I immediately decided to extend it as a square+cube+hypercube task in arbitary dimensions!
Math Fun: On the Geometry of 3D and 4D space
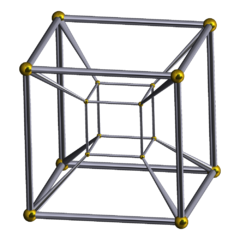
Hey, do allow me introduce two cool terms I recently learnt: "ana" and "kata". In an Euclidean 3D space, which most of us believe ourselves are familiar with, we can have Up/Down/North/East/South/West (or Up/Down/Back/Left/Front/Right, esp. if you have played Rubik's Cube). In 4D, there is one more axis, thus two more directions we can have, and some mathematicians assign "ana" and "kata" as the names for those directions.
[Need not to fancy too much about "time as the fourth dimension"… The "metric" for measuring distance used by physicists for the dimension of time is called Minkowski metric (generalized: Lorentzian metric). And that "4D world" is called Minkowski spacetime.]
In my submitted codes, A/K/U/D/N/E/S/W are used; the South-East-Down point is picked to be the initial point for vector calculation in 3D and the Kata-South-East-Down point is picked for the same purpose in 4D.
Properties of Squares (and Cubes) and a Primitive Algorithm
A quadrilateral with 4 sides equal can be a rhombus but not a square.
A polyhedron with its 12 sides equal can be a parallelepiped but not a cube.
To conclude, we have to get more details besides calculations of the lengths of edges.
Before jumping to the next section about cube-check and hypercube-check, we may have to consider checking for the square first.
Let a be the length of an edge of the regular "cube-like" polytope.
Though edges are not sufficient conditions for proving/disproving whether a polytope(the umbrella term for polygon, polyhedron, …) is a "cube-like" polytope, it seems that we must know their lengths and check whether they are equal. All we have on hand is the coordinates of vertices, without given their "order" in the plane/space.
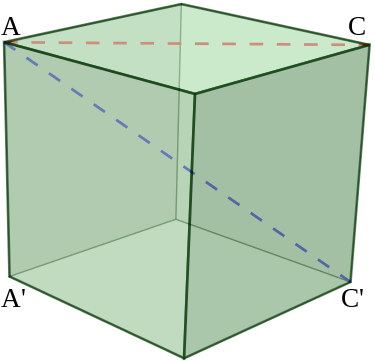
Discuss the case of a square. We name the vertices are p0, p1, p2, and p3. We have the segment between pm and pn can be either an edge or a diagonal. We have 6 segments to consider. And we know from high school math that sqrt(2)*a is the length of the diagonal.
As mentioned, an edge-equal quadrilaternal can be a rhombus. But if we additionally consider the length of diagonals, the square has equal-length diagonals and an arbitarily constructed rhombus usually does not. Hence we can have a simple algorithm:
say is_square($pt0, $pt1, $pt2, $pt3);
sub is_square {
my ($p0,$p1,$p2,$p3) = ($_[0], $_[1], $_[2], $_[3]);
... code block calculate the vectors pairwisely
my @n_vector = map { norm($_) } ($v0, $v1, $v2, ... );
@n_vector = sort {$a<=>$b} @n_vector;
if the first four items of @n_vector are equal
and the last two items of @n_vector are equal
then return 1
else return 0
}
sub norm {
my $p = $_[0];
my $sum = 0;
$sum+= ($p->[$_])**2 for (0..$p->$#*);
return $sum;
}
ok is_square( [10,20], [20,20], [20, 10], [10, 10] ) == 1, "Example 1";
ok is_square( [12,24], [16,10], [20, 12], [18, 16] ) == 0, "Example 2";
ok is_square( [1, 2] , [4,3], [3,1], [2,4] ) == 1, "Knight's square";
ok is_square( [1, 1] , [-1, 1], [ 1,-1], [-1,-1] ) == 1, "centre at origin";
Math Fun: Properties of n-hypercube
Shouldn’t we investigate some basic stuff about the cube in order to understand the hypercube?
Cube:
Number of vertices: 8
Number of edges: 12
Number of faces: 6
Number of cubes: 1
Especially for the segments between pairs of vertices:
Number of edges: 12
Number of face diagonals: 12
Number of body diagonals: 4
Total Number of Segments: 28
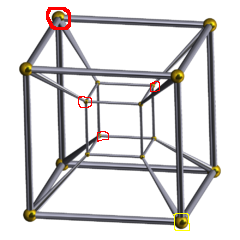
Look at the diagram of the hypercube on right in order to get some sensation on it.
Now we proceed (can be counted from looking at the diagram):
Hypercube:
Number of vertices: 8 × 2 = 16
Number of edges: num of edges in a cube × 2 + 8 edges from the self replicating process = 12×2 + 8 = 32
Number of faces: num of faces in a cube × 2 + 12 faces new = 6×2 + 4×6÷2 = 24
Number of cubes: 2 + 6 = 8
Especially for the segments between pairs of vertices:
Number of edges: 32
Number of face diagonals: 2×24 = 48
Number of body diagonals: 4×8 = 32
Number of "hyperdiagonals": 8
Total Number of Segments: 120
I have circled the four body-diagonal points with respect to the bigger bottom right point in red colour as I think it might be the most difficult for us to catch them by intuition.
Though we are not going to code for the 5-hypercube, we may try some calculations based on above.
5-hypercube. Yup, disclamier: I cannot "sense" how the 5-hypercube looks like. Here are just calculations (number of edges verified on OEIS sequence A001787 :
Number of vertices: 32
Number of edges: 32×2 + 16 = 80
Number of faces: 20×2 + ? × ? ÷ ? = ??
Oh, I resign, I fail to continue to count the remaining! But we can see there are already 80 edges, we can expect an order of magnitude of 102 or above for the total number of concerned segments in 5-hypercube.
Vector Sum Approach
As said, we cannot solely rely on the length of edges. And the section "Properties of Squares (and Cubes) and a Primitive Algorithm" has already provided an algorithm and codes, what am I going to talk about?
If you read the optional section Properties of n-hypercube" you will find there would be a huge number of length of segments we are going to calculate if we follow the primitive algorithm.
Another side of the primitive algorithm we need to consider is: are there any polytope with same various diagonals which are the same? Intuitively the answer is yes, but… I haven’t proved it. So it remains a "conjecture" in our context. So… I don’t think it is a safe approach for extending to cube or hypercube. A safer approach under the condition that "the diagonal conjecture is not yet proved" is checking the norm of a diagonal against the norm of an edge.
OK let us see the code now:
sub is_square {
my ($p0,$p1,$p2,$p3) = ($_[0], $_[1], $_[2], $_[3]);
my $v0 = vec_subtract($p0, $p1);
my $v1 = vec_subtract($p0, $p2);
my $v2 = vec_subtract($p0, $p3);
# "dot product test";
# return 0 unless (vec_prod_f($v1, $v2) == 0) xor
# (vec_prod_f($v0, $v2) == 0) xor
# (vec_prod_f($v0, $v1) == 0);
my @n_vector = map { norm($_) } ($v0, $v1, $v2);
@n_vector = sort {$a<=>$b} @n_vector;
# "norm test"
#if ( $n_vector[0] == $n_vector[1] ) {
# the above conditional is fit for integter coordinates
# the below is special arrangement starting from the 5th test case
# or floating point number in general
if ( sprintf("%f",$n_vector[0]) == sprintf("%f", $n_vector[1])
&& 2*sprintf("%f", $n_vector[0]) == sprintf("%f", $n_vector[2])
# the above line concerning length of diagonal is sqrt(2)
# times the edge length would not be a necessary check
# if we preserve the dot product test, because in
# Euclidean space, if two vectors are orthogonal and in equal length,
# we can apply the Pythagorean theorem for the norm of the vector sum.
# For DEMOSTRATION PURPOSE,
# the test of orthogonality (the dot product test) is commented out by brace,
# but the dot product test will be used both for cube and hypercube.
) {
return 1;
}
return 0;
}
sub vec_prod {
my $first = $_[0];
my $second = $_[1];
warn "Not the same dimension in vec_prod \n" if $first->$#* != $second->$#*;
my $sum = 0;
$sum+= ($first->[$_]*$second->[$_]) for (0..$first->$#*);
return $sum;
}
sub vec_subtract {
my $first = $_[0];
my $second = $_[1];
my $ans = [];
warn "Not the same dimension in vec_subtract\n" if $first->$#* != $second->$#*;
for my $s (0..$first->$#*) {
push $ans->@*, $second->[$s] - $first->[$s];
}
return $ans;
}
By the properties of vectors, the diagonal vector is the vector sum of two vectors representing the edge while we are keeping the direction correctly.
I will discuss the ugly &sprintf() (gonna be replaced by &norm_f ) on the later section "Numerical Inaccuracy". See also the reason of not using dot product test; honestly I am not sure which (dot product test or checking the norms) is a better combat against numerical inaccuracy; therefore they are being "comment out" via =pod.
Adventure to Cube and Hypercube
I intentionally avoid using permutations in the &is_cube here but using permtutations in &is_hypercube for DEMOSTRATING the logic more explicitly for some potential audience. Three nested conditionals, acceptable (?). You can get the link for finalized, more concise code at the bottom of the page.
sub is_cube {
my @p = @_;
my %v;
$v{$_} = vec_subtract($p[0], $p[$_]) for (1..7);
my @ind = sort { norm($v{$a}) <=> norm($v{$b}) } keys %v;
my ($N, $W, $U) = ($v{$ind[0]} , $v{$ind[1]} , $v{$ind[2]}) ;
return 0 unless norm_f($N) == norm_f($W) && norm_f($N) == norm_f($U);
return 0 unless vec_prod_f($N,$W) == 0 && vec_prod_f($W,$U) == 0
&& vec_prod_f($U,$N) == 0;
my $NW = vec_sum($N, $W);
my $WU = vec_sum($W, $U);
my $UN = vec_sum($U, $N);
my $bool = undef;
if (vec_same_f($NW, $v{$ind[3]})) {
if ( vec_same_f($WU, $v{$ind[4]})
&& vec_same_f($UN, $v{$ind[5]}) ) { $bool = 1;
} elsif ( vec_same_f($WU, $v{$ind[5]})
&& vec_same_f($UN, $v{$ind[4]}) ) { $bool = 1;
}
}
if (!$bool && vec_same_f($NW, $v{$ind[4]})) {
if ( vec_same_f($WU, $v{$ind[3]})
&& vec_same_f($UN, $v{$ind[5]}) ) { $bool = 1;
} elsif ( vec_same_f($WU, $v{$ind[5]})
&& vec_same_f($UN, $v{$ind[3]}) ) { $bool = 1;
}
}
if (!$bool && vec_same_f($NW, $v{$ind[5]})) {
if ( vec_same_f($WU, $v{$ind[4]})
&& vec_same_f($UN, $v{$ind[3]}) ) { $bool = 1;
} elsif ( vec_same_f($WU, $v{$ind[3]})
&& vec_same_f($UN, $v{$ind[4]}) ) { $bool = 1;
} else {
return 0;
}
}
return 0 if !$bool;
my $NWU = vec_sum( $N, $WU);
if ( vec_same_f( $v{$ind[6]} , $NWU ) ) {
=pod
return 0 unless
2*norm_f($N) == norm_f($NW) &&
norm_f($NW) == norm_f($WU) &&
norm_f($WU) == norm_f($UN) &&
3*norm_f($N) == norm_f($NWU);
=cut
return 1;
}
else {
return 0;
}
}
sub is_hypercube {
my @p = @_;
my %v;
$v{$_} = vec_subtract($p[0], $p[$_]) for (1..15);
my @ind = sort { norm($v{$a}) <=> norm($v{$b}) } keys %v;
my ($N, $W, $U, $A) = ( $v{$ind[0]}, $v{$ind[1]} ,
$v{$ind[2]}, $v{$ind[3]} );
return 0 unless
norm_f($N) == norm_f($W) && norm_f($W) == norm_f($U)
&& norm_f($U) == norm_f($A);
return 0 unless
vec_prod_f($N, $W) == 0 &&
vec_prod_f($N, $U) == 0 &&
vec_prod_f($N, $A) == 0 &&
vec_prod_f($A, $W) == 0 &&
vec_prod_f($A, $U) == 0 &&
vec_prod_f($W, $U) == 0 ;
my $AU = vec_sum($A, $U);
my $AW = vec_sum($A, $W);
my $AN = vec_sum($A, $N);
my $NW = vec_sum($N, $W);
my $WU = vec_sum($W, $U);
my $UN = vec_sum($U, $N);
my $bool_face = undef;
my $iter_face = permutations([$AU, $UN, $NW, $WU, $AW, $AN]);
while (!$bool_face && (my $p = $iter_face->next)) {
$bool_face =
vec_same_f($v{$ind[4]}, $p->[0]) &&
vec_same_f($v{$ind[5]}, $p->[1]) &&
vec_same_f($v{$ind[6]}, $p->[2]) &&
vec_same_f($v{$ind[7]}, $p->[3]) &&
vec_same_f($v{$ind[8]}, $p->[4]) &&
vec_same_f($v{$ind[9]}, $p->[5]) ;
}
return 0 if !$bool_face;
my $UNW = vec_sum($UN, $W);
my $ANW = vec_sum($NW, $A);
my $AWU = vec_sum($WU, $A);
my $AUN = vec_sum($UN, $A);
my $bool_cube = undef;
my $iter_cube = permutations([$UNW, $ANW, $AWU, $AUN]);
while (!$bool_cube && (my $p = $iter_cube->next)) {
$bool_cube =
vec_same_f($v{$ind[10]}, $p->[0]) &&
vec_same_f($v{$ind[11]}, $p->[1]) &&
vec_same_f($v{$ind[12]}, $p->[2]) &&
vec_same_f($v{$ind[13]}, $p->[3]);
}
return 0 if !$bool_cube;
my $AUNW = vec_sum($AU,$NW);
if ( vec_same_f($v{$ind[14]}, $AUNW) ) {
=pod
return 0 unless
2*norm_f($N) == norm_f($NW) &&
norm_f($NW) == norm_f($AU) &&
norm_f($NW) == norm_f($UN) &&
norm_f($NW) == norm_f($WU) &&
norm_f($NW) == norm_f($AW) &&
norm_f($NW) == norm_f($AN) &&
3*norm_f($N) == norm_f($UNW) &&
3*norm_f($N) == norm_f($ANW) &&
3*norm_f($N) == norm_f($AWU) &&
3*norm_f($N) == norm_f($AUN) &&
4*norm_f($N) == norm_f($AUNW);
=cut
return 1;
}
else {
return 0;
}
}
Numerical Inaccuracy
When all the coordinates are integers, there will not be any problems. What if we supply sqrt($INT) or sin($ANGLE)? It was found that Perl 5 (maybe many other programming language which are not built-in radical or "good sin function"). does not work well. Luckily a roundabout is found:
sprintf("%f", $non-integer-value).
sub vec_prod {
my $first = $_[0];
my $second = $_[1];
warn "Not the same dimension in vec_prod \n" if $first->$#* != $second->$#*;
my $sum = 0;
$sum+= ($first->[$_]*$second->[$_]) for (0..$first->$#*);
return $sum;
}
sub vec_prod_f {
return sprintf("%f", vec_prod($_[0], $_[1]));
}
sub norm {
my $p = $_[0];
my $sum = 0;
$sum+= ($p->[$_])**2 for (0..$p->$#*);
return $sum;
}
sub norm_f {
return sprintf("%f", norm($_[0]));
}
sub vec_same {
my $first = $_[0];
my $second = $_[1];
warn "Not the same dimension in vec_same\n" if $first->$#* != $second->$#*;
for my $s (0..$first->$#*) {
return undef if $first->[$s] != $second->[$s];
}
return 1;
}
sub vec_same_f {
my $first = $_[0];
my $second = $_[1];
warn "Not the same dimension in vec_same_f\n" if $first->$#* != $second->$#*;
for my $s (0..$first->$#*) {
return undef if sprintf("%f",$first->[$s]) != sprintf("%f",$second->[$s]);
}
return 1;
}
Discussion for the Norm-ONLY Approach
It is possible to calculate all the lengths between points, sort them, and compare whether a cluster of them is equally valued (or whether they are correct multiples of the length of the edges). However, the number of total segments exponentially increases as the dimension increases. And I don’t know yet what the minimum number of segment length to be checked is (except for squares).
Another mathematical point is, if we fix a point as "reference origin", we only need to calculate and sort 2N-1 vectors. Not out of surprise is that the distribution of lengths of the vectors follow the Pascal triangle:
For N = 2, check (1) diagonal;
For N = 3, check (2, 1) diagonals;
For N = 4, check (3, 3, 1) diagonals;
For N = 5, check (4, 6, 4, 1) diagonals;
...
If we calculate all the segments, there are 2N-1 × (2N-1) segments, and the distribution of the lengths is a bit more unpleasant to be calculated:
For N = 2, check (2) diagonals;
For N = 3, check (12, 4) diagonals;
For N = 4, check (48, 32, 8) diagonals;
Summary
I don’t do the &is_5-hypercube. But you can see it will be about checking the orthogonality of the set of 31 vectors origined from one of the vertices, sorting their norms; just bear in mind that the distribution of the lengths of the vectors is (5, 10, 10, 5, 1), check whether the vector sums of the edges are same as diagonals…
If you have any suggestion then please do share with us perlweeklychallenge@yahoo.com.
