Raku Solutions Weekly Review
Task #1: Computing the Digits of Pi
This is derived in part from my blog post made in answer to the Week 04 of the Perl Weekly Challenge organized by Mohammad S. Anwar as well as answers made by others to the same challenge.
The challenge reads as follows:
Write a script to output the same number of PI digits as the size of your script. Say, if your script size is 10, it should print 3.141592653.
My Solutions
Let’s start with a simple one-liner satisfying the requirement:
perl6 -e '
print pi, "\n";
'
3.14159265358979
So, job done? Well, yes and no. Let’s try to be more serious and adapt the size of our output to the size of the script, which means to actually calculate some digits of pi.
I’ve tried several formulae known for centuries (François Viète, John Wallis, John Machin, Isaac Newton, Gottfried Wilhelm Leibniz, etc.), but will show only one of them to illustrate the problem.
John Wallis’s infinite product can be reformatted as:
pi / 2 = (2 * 2 * 4 * 4 * 6 * 6 * 8 * 8 ... ) / (1 * 3 * 3 * 5 * 5 * 7 * 7 * 9 ...)
We can build two lazy infinite lists, one for the numerator and one for the denominator and use the reduction operator to calculate Wallis’s infinite product:
my @numerators = 2, 2, -> $a, $b {| ($a + 2, $b + 2) } ... *;
my @denominators = 1, 3, 3, -> $a, $b {| ($a + 2, $b + 2) } ... *;
my $pi = 2 * ([*] @numerators[0..2000]) / ([*] @denominators[0..2000]);
The value obtained for $pi is:
3.14237736509388
Only the first three digits are correct with a product of two thousands terms! Quite obviously, those century-old formulas converge much too slowly for our purpose. We need something more efficient.
The Indian mathematician Srinivasa Ramanujan is known as the author of a number of innovative new formulae for calculating digits of pi during the first decades of the twentieth century, but the one I looked at is not so easy to implement, notably because it involves the square root of two, so we would need to start by calculating the digits of that number as a FatRat. This is the solution adopted by Doug Schrag (see below in the Alternative Solutions section), but I decided to take another approach.
In 2006, Franco-Canadian mathematician Simon Plouffe used the so-called PSLQ integer relation algorithm to generate several new formulae for pi. One of them was described back in 1995 and is known as one of the spigot algorithms.
We can write the following plouffe subroutine:
sub plouffe (Int $k) {
my $result = (1 / 16 ** $k) * ( (4 / (8 * $k + 1)) - (2 / (8 * $k + 4)) - (1 / (8 * $k + 5)) - (1 / (8 * $k + 6) ) );
}
to calculate the individual terms of the infinite sum and then compute pi as follows:
my $pi = [\+] (plouffe $_ for 0..20);
That does not work properly, however, as the plouffe terms get converted from rationals to floats (well, really from Rat to Num) when the input value reaches 11 or more, as shown here under the REPL:
> say (plouffe $_).WHAT for 0..15;
(Rat)
(Rat)
(Rat)
(Rat)
(Rat)
(Rat)
(Rat)
(Rat)
(Rat)
(Rat)
(Rat)
(Num)
(Num)
(Num)
(Num)
(Num)
so that we are losing accuracy and the result:
3.141592653589793129614170564041344859
is correct only up to the 16th digit.
So, let’s try to use the FatRat type:
sub plouffe (Int $k) {
my $result = 1.FatRat * (1 / 16 ** $k) * ( (4 / (8 * $k + 1)) - (2 / (8 * $k + 4)) - (1 / (8 * $k + 5)) - (1 / (8 * $k + 6) ) );
}
It is a bit better, but we are again falling back to Num when the subroutine input value reaches 17 or above:
> say (plouffe $_).WHAT for 0..20;
(FatRat)
(FatRat)
(FatRat)
(FatRat)
(FatRat)
(FatRat)
(FatRat)
(FatRat)
(FatRat)
(FatRat)
(FatRat)
(FatRat)
(FatRat)
(FatRat)
(FatRat)
(FatRat)
(Num)
(Num)
(Num)
(Num)
(Num)
For some reason, coercing the input value to a FatRat:
sub plouffe (FatRat $k) {
my $result = (1 / 16 ** $k) * ( (4 / (8 * $k + 1)) - (2 / (8 * $k + 4)) - (1 / (8 * $k + 5)) - (1 / (8 * $k + 6) ) );
}
say (plouffe $_.FatRat).WHAT for 0..20;
doesn’t work either.
While still trying to understand why we are falling from FatRat to Num, I posted a question on perl6-users, and I quickly received very useful tips from Fernando Santagata and Brian Duggan. Many thanks to them.
The following syntax suggested by Brian works properly:
sub plouffe (Int $k) {
my $result = (1.FatRat / 16 ** $k) * ( (4 / (8 * $k + 1)) - (2 / (8 * $k + 4)) - (1 / (8 * $k + 5)) - (1 / (8 * $k + 6) ) );
}
# printing 200 digits of pi
my $pi = [+] (plouffe $_ for 0..200);
Now, $pi is populated with about 750 digits, two thirds of which are wrong, but the important point is that they are all correct up to the 249th digit. In general, we get an average of about 1.2 correct digits per term in the sum. So, with the above input values, we’re on the safe side of things if we print out the first two hundred digits under the REPL:
> say substr $pi, 0, 201;
3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679821480865132823066470938446095505822317253594081284811174502841027019385211055596446229489549303819
It is now fairly easy to output the same number of PI digits as the size of the script:
sub plouffe (Int $k) {
my $result = (1.FatRat / 16 ** $k) * ( (4 / (8 * $k + 1)) - (2 / (8 * $k + 4)) - (1 / (8 * $k + 5)) - (1 / (8 * $k + 6) ) );
}
my $script-size = $*PROGRAM-NAME.IO.s;
my $pi = [+] (plouffe $_ for 0..$script-size);
say substr $pi, 0, $script-size + 1; # +1 because the decimal dot isn't a digit
The script has 290 bytes and the script prints the first 290 digits of pi:
$ perl6 pi.p6
3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679821480865132823066470938446095505822317253594081284811174502841027019385211055596446229489549303819644288109756659334461284756482337867831652712019091456485669234603486104543266482133936072
The script runs in slightly less than 1.5 sec.
Alternative Solutions
Arne Sommer provided a solution very similar to my initial one-liner:
say pi.fmt('%.19f')
He also suggested another solution using the following PiXL.pm6module:
use v6.d;
unit module PiXL;
our constant $PI is export = "3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679821480865132823066470938446095505822317253594081284811174502841027019385211055596446229489549303819644288109756659334461284756482337867831652712019091456485669234603486104543266482133936072602491412737245870066063155881748815209209628292540917153643678925903600113305305488204665213841469519415116094330572703657595919530921861173819326117931051185480744623799627495673518857527248912279381830119491298336733624406566430860213949463952247371907021798609437027705392171762931767523846748184676694051320005681271452635608277857713427577896091736371787214684409012249534301465495853710507922796892589235420199561121290219608640344181598136297747713099605187072113499999983729780499510597317328160963185950244594553469083026425223082533446850352619311881710100031378387528865875332083814206171776691473035982534904287554687311595628638823537875937519577818577805321712268066130019278766111959092164201989";
and then used the module as follows:
use lib "lib";
use PiXL;
say $PI.substr(0, $?FILE.IO.s -1);
The trick is clear: store so many digits of pi as you want in a separate module, since the size of the module will not counted in the script size.
Jo Christian Oterhals used essentially the same trick and first created the following BigPi.pm6 module:
# Perl 6 Module BigPI.pm6
# Place in script directory and use perl6 with -I flag
# i.e. perl6 -I. <calling script>
unit module BigPI;
# This definition of PI is taken from the Perl 5 module Math::BigFloat
constant PI = join '', qw:to/END/;
314159265358979323846264338327950288419716939937510582097494459230781640628
620899862803482534211706798214808651328230664709384460955058223172535940812
848111745028410270193852110555964462294895493038196442881097566593344612847
564823378678316527120190914564856692346034861045432664821339360726024914127
372458700660631558817488152092096282925409171536436789259036001133053054882
046652138414695194151160943305727036575959195309218611738193261179310511854
807446237996274956735188575272489122793818301194912983367336244065664308602
139494639522473719070217986094370277053921717629317675238467481846766940513
200056812714526356082778577134275778960917363717872146844090122495343014654
958537105079227968925892354201995611212902196086403441815981362977477130996
051870721134999999837297804995105973173281609631859502445945534690830264252
230825334468503526193118817101000313783875288658753320838142061717766914730
359825349042875546873115956286388235378759375195778185778053217122680661300
192787661119590921642019893809525720106548586327886593615338182796823030195
END
and then used it as follows:
use BigPI;
say BigPI::pi $?FILE.IO.s;
Joelle Maslak also hard-coded the digits of pi but had the clever idea of using a base-32 representation of pi, thus making the script shorter:
say 3~'.'~:32<35IPR975H1E3E2K2GQK0D32I3C1U7N>
This works properly as shown under the REPL:
> say 3~'.'~:32<35IPR975H1E3E2K2GQK0D32I3C1U7N>
3.141592653589793238462643383279502884197169399
Doug Schrag based his calculation of a formula discovered by Srinivasa Ramanujan:
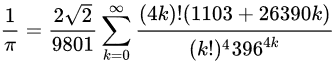
For this, he first implemented a sqrt-rat subroutine to compute a FatRat estimate of the square root of 2:
my $chars = $*PROGRAM.slurp.chars;
say pi-rat.Str.substr(0,$chars);
say "$chars digits!";
sub postfix:<!> ($n) { [*] 1..$n }
sub f($k) {
FatRat.new: (4*$k)! * (1103 + 26390 * $k), ($k!)**4 * 396**(4*$k)
}
sub pi-rat () {
9801 * sqrt-rat(2, 1e-500) / 4
/ [+] (^80).map: *.&f
}
multi sub sqrt-rat ($n where * > 0, $eps) {
my $base = $n.FatRat($eps);
my $r = sqrt($base).FatRat($eps);
my $est;
repeat {
$est = $r;
$r = ($base / $est + $est) / 2;
} while abs($r - $est) > $eps;
return $r;
}
multi sub sqrt-rat (0) { 0 }
Francis J. Whittle apparently based his computation on the Newton-Euler convergence transformation formula:
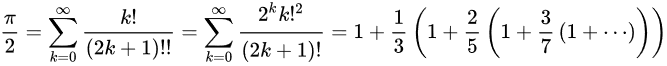
where (2k + 1)!! denotes the product of the odd integers up to 2k + 1.
His program first computes a lazy list of the various terms of the sum and then multiplies by two the sum of the 608 first terms:
my $eu-seq = gather {
take 1;
for 1..* -> $n { take $eu-seq[$n - 1] * FatRat.new($n, 2 * $n + 1) }
}
my \π := 2 * [+] $eu-seq[^608];
put π.Str.substr: ^($?FILE.IO.s+1);
Jaldhar H. Vyas provided a very simple solution using the Rat::Precise module:
# Thanks to thundergnat for the module and informing me about it on IRC.
use Rat::Precise;
my $size = $*PROGRAM-NAME.IO.s;
π.FatRat.precise($size - 1).say; # - 1 because 3. is a digit of pi
I also did not know about that module, so thanks to thundergnat and to Jaldhar for the information.
James A. Smith provided a solution similar to my initial one-liner:
say 2*atan2 1,0;
Actually, this almost exactly the idea I suggested in my Perl 5 solution.
Nick Logan submitted a polyglot script, i.e. a script running both in Perl 5 and Perl 6:
# WARNING: this polyglot breaks best practices of both Perl 5 and Perl 6 in order to run on both
sub eval($_) { &EVAL($_) };
sub polyint($_) { "0" and (return Int($_[0])) or (return int($_[0])) };
sub script_size { "0" and (return 0+eval('$*PROGRAM.IO.s')) or (return 0+eval('-s $0')) };
#`() use isms; sub infix:«<<»($a,$b) { $a +< $b };
my $digits = script_size() + 1;
my (@out, @a);
my ($b, $c, $d, $e, $f, $g, $i, $d4, $d3, $d2, $d1);
$b = $d = $e = $g = $i = 0;
$f = 10000;
$c = 14 * (polyint($digits/4)+2);
print "3.";
while (($b = $c -= 14) > 0 && $i < $digits) {
$d = $e = $d % $f;
while (--$b > 0) {
$d = $d * $b + (@a[$b] // 20000000);
$g = ($b << 1) - 1;
@a[$b] = ($d % $g) * $f;
$d = polyint($d / $g);
}
$d4 = $e + polyint($d/$f);
if ($d4 > 9999) {
$d4 -= 10000;
@out[$i-1]++;
$b = $i-1;
while (@out[$b] == 1) {
@out[$b] = 0;
@out[$b-1]++;
$b--;
}
}
$d3 = polyint($d4/10);
$d2 = polyint($d3/10);
$d1 = polyint($d2/10);
@out[$i++] = $d1;
@out[$i++] = $d2-$d1*10;
@out[$i++] = $d3-$d2*10;
@out[$i++] = $d4-$d3*10;
print join "", @out[$i-15 .. $i-15+3] if $i >= 16;
}
print join "", @out[$i-15+4 .. $digits-2], "\n";
Rob4t used basically the same idea as in my initial one-liner:
say π;#size 16
Ruben Westerberg used, if I understand well, one of the numerous continued fraction formulae:
#!/usr/bin/env perl6
my $places= $*PROGRAM-NAME.IO.s + 1;
printf "Places: $places\n";
my $prev="";
my $sign;
my $pi=(0/1).FatRat;
my $denom=1;
my $stable= 0;
my $i=0;
my $float;
until ($stable) {
$sign= (($i %% 2) ?? 4 !! -4);
$pi+=($sign/$denom).FatRat;
$denom+=2;
$i++;
$float=$pi.Str.substr(0,$places+1);
say "Iteration: $i, Value of PI (to $places decimal places):$float";
$stable=$float eq $prev;
$prev=$float;
}
Mark Senn used the same formula by Simon Plouffe formula as I did:
sub plouffe (Int $k)
{
(1.FatRat/16**$k) *
(
(4 / (8*$k + 1))
- (2 / (8*$k + 4))
- (1 / (8*$k + 5))
- (1 / (8*$k + 6))
)
}
# Get size of the script.
my $size = $*PROGRAM-NAME.IO.s;
# The value of pi has only been double
# checked up to 1000 characters.
if ($size > 1_000)
{
die "program not tested for a "
~ "script size of more than "
~ "1000 characters";
}
my $pi = [+] (plouffe $_ for 0..$size);
say substr($pi, 0, $size);
Mark acknowledges in his blog post that he was prompted to use this formula by my question on perl6-users and the answers provided by Fernando Santagata and Brian Duggan.
Simon Proctor created a /// operator to transform simple division into FatRat constructor and assignment, thus avoiding the Rat falling to Num problem I reported at the beginning of this post. Otherwise, he used the same Plouffe formula as I did:
sub infix:<///> ( Int() $nu, Int() $de ) { FatRat.new( $nu, $de ) }
sub bbp-digit ( Int $k ) {
my $k8 = $k*8;
(1 /// (16 ** $k)) * ((4 /// ($k8 + 1)) - (2 /// ($k8 + 4)) - (1 /// ($k8 + 5)) - (1 /// ($k8+6)));
}
sub calc-pi( Int $num ) {
my $p = [+] ( 0..$num ).map( &bbp-digit );
return $p.Str.substr(0,$num+1);
}
#| Calculate PI to a given number of digits
sub MAIN (
Int $digits #= Number of digits to calcuate
) {
say calc-pi( $digits );
}
Simon was also reports in his blog post that he was prompted to use this formula by my question on perl6-users and the answers provided by Fernando Santagata and Brian Duggan.
Tim Smith used another so-called spigot algorithm like so:
#| http://www.cs.ox.ac.uk/people/jeremy.gibbons/publications/spigot.pdf
sub gibbons-spigot() {
my ($q, $r, $t, $i) = 1, 180, 60, 2;
gather loop {
my $u = 3 * (3 * $i + 1) * (3 * $i + 2);
my $y = floor(($q * (27 * $i - 12) + 5 * $r) / (5 * $t));
take $y;
($q, $r, $t, $i) =
10 * $q * $i * (2 * $i - 1),
10 * $u * ($q * (5 * $i - 2) + $r - $y * $t),
$t * $u,
$i + 1;
}
}
SEE ALSO
Four blog posts on the subject:
-
Arne Sommer: https://perl6.eu/piermutations.html;
-
Simon Proctor: https://www.khanate.co.uk/blog/2019/04/21/perl-weekly-week-4/;
-
Jo Christian Oterhals: https://medium.com/@jcoterhals/perl-6-small-stuff-17-a-weekly-challenge-of-big-pis-bags-and-modules-6c6c0867cb0a.
Wrapping up
Please let me know if I forgot any of the challengers or if you think my explanation of your code misses something important (send me an e-mail or just raise an issue against this GitHub page).
